Baseline-determination
Due to the high electron cross-section, background signals (or baseline) are much more of a problem for electron diffraction than equivalent X-ray experiments.
In the case of polycrystalline samples (i.e. 1D diffraction signals), the definite way of removing background signals is to use an iterative approach based on the dual-tree complex wavelet transform. Consider the following example polycrystalline vanadium dioxide pattern:
(Source code, png, hires.png, pdf)
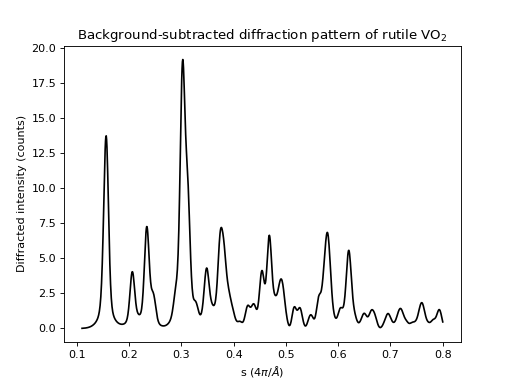
It would be very difficult to interpolate a background from elastic scattering-free regions of the diffraction pattern, and this is a moderately We can add a background typical of silicon nitride substrates, as well as inelastic scattering effects:
>>> from skued import gaussian
>>> import numpy as np
>>>
>>> s, intensity = np.load("docs/tutorials/data/powder.npy")
>>>
>>> background = 75 * np.exp(-7 * s) + 55 * np.exp(-2 * s)
>>> substrate1 = 0.8 * gaussian(s, center = s.mean(), fwhm = s.mean()/4)
>>> substrate2 = 0.9 * gaussian(s, center = s.mean()/2.5, fwhm = s.mean()/4)
(Source code, png, hires.png, pdf)
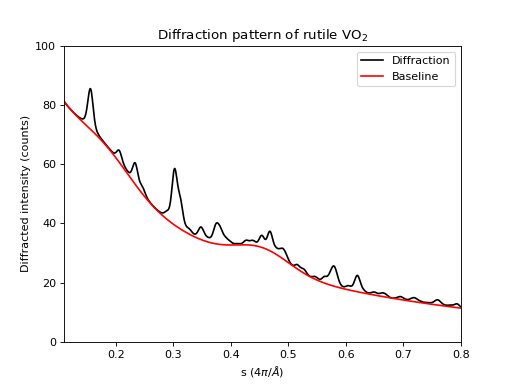
Scikit-ued offers two ways of removing the background.
Iterative Baseline Determination using the Discrete Wavelet Transform
The procedure and rational for the baseline_dwt() routine is described in detail in:
Galloway et al. ‘An Iterative Algorithm for Background Removal in Spectroscopy by Wavelet Transforms’, Applied Spectroscopy pp. 1370 - 1376, September 2009.
Here is a usage example for the data presented above:
>>> import numpy as np
>>> from skued import gaussian
>>> from skued import baseline_dwt
>>>
>>> s, intensity = np.load("docs/tutorials/data/powder.npy")
>>>
>>> # Double exponential inelastic background and substrate effects
>>> diffuse = 75 * np.exp(-7 * s) + 55 * np.exp(-2 * s)
>>> substrate1 = 0.8 * gaussian(s, center = s.mean(), fwhm = s.mean()/4)
>>> substrate2 = 0.9 * gaussian(s, center = s.mean()/2.5, fwhm = s.mean()/4)
>>>
>>> baseline = baseline_dwt(s, level = 6, max_iter = 150, wavelet = 'sym6')
(Source code, png, hires.png, pdf)
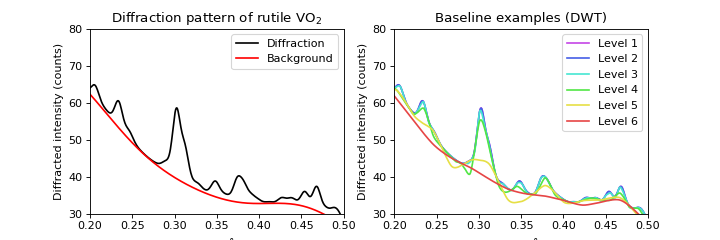
Iterative Baseline Determination using the Dual-Tree Complex Wavelet Transform
In the case of 1D data (or along a 1D axis), there is a more performant alternative to baseline_dwt(). The
dual-tree complex wavelet transform improves on the discrete wavelet transform in many ways.
Therefore, the method presented in this section should be preferred.
For more information on the why and how, please refer to:
L. P. René de Cotret and B. J. Siwick, A general method for baseline-removal in ultrafast electron powder diffraction data using the dual-tree complex wavelet transform, Struct. Dyn. 4 (2017)
Here is a usage example for the data presented above:
>>> import numpy as np
>>> from skued import gaussian
>>> from skued import baseline_dt
>>>
>>> s, intensity = np.load("docs/tutorials/data/powder.npy")
>>>
>>> # Double exponential inelastic background and substrate effects
>>> diffuse = 75 * np.exp(-7 * s) + 55 * np.exp(-2 * s)
>>> substrate1 = 0.8 * gaussian(s, center = s.mean(), fwhm = s.mean()/4)
>>> substrate2 = 0.9 * gaussian(s, center = s.mean()/2.5, fwhm = s.mean()/4)
>>>
>>> baseline = baseline_dt(s, wavelet = 'qshift3', level = 6, max_iter = 150)
(Source code, png, hires.png, pdf)
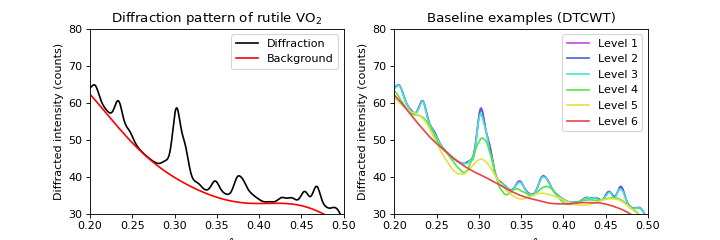
The baseline_dt() routine will usually be more accurate than its baseline_dwt() counterpart.