Image Analysis/Processing

Diffraction patterns analysis is essentially specialized image processing. This tutorial will show some of the image processing and analysis techniques that are part of the scikit-ued.

Note

Use scikit-ued in combination with npstreams to process electron diffraction data in parallel.

Reading Images

Diffraction patterns can come in a variety of exotic file formats. Scikit-ued has built-in support for the following file formats:

  • Gatan’s closed source DM3 and DM4 (*.dm3, *.dm4);

  • Merlin Image Binary (*.mib);

  • TIFF images (*.tif, *.tiff);

  • All other file formats supported by scikit-image.

The diffread() function will transparently distinguish between those formats and dispatch to the right functions.

Automatic center-finding

Many analyses involving diffraction patterns require the knowledge of the center. For this purpose, scikit-ued provides autocenter(). It can be used trivially as follows:

>>> from skued import diffread, autocenter
>>> import numpy as np
>>>
>>> im = diffread('docs/tutorials/data/Cr_1.tif')
>>>
>>> # Invalid pixels are masked with a False
>>> mask = np.ones_like(im, dtype = bool)
>>> mask[0:1250, 975:1225] = False
>>>
>>> center = autocenter(im, mask=mask)

Let’s take a look at the result. The center is shown with a red dot:

(Source code, png, hires.png, pdf)

../_images/image-1.png

We can do the same with single-crystal diffraction patterns:

>>> from skued import diffread, autocenter
>>> import numpy as np
>>>
>>> im = diffread('docs/tutorials/data/graphite.tif')
>>> mask = diffread('docs/tutorials/data/graphite_mask.tif').astype(bool)
>>>
>>> center = autocenter(im, mask=mask)

Let’s take a look at the result. The center is shown with a red dot:

(Source code, png, hires.png, pdf)

../_images/image-2.png

autocenter() also works with images that are very off-center and display large Ewald-sphere walkoff:

(Source code, png, hires.png, pdf)

../_images/image-3.png

It’s worth emphasizing that apart from the mask, there are no parameters to play with; autocenter() is as automatic as it can be!

Diffraction pattern alignment

Diffraction patterns can drift over a period of a few minutes, and for reliable data synthesis it is important to align patterns to a reference.

Diffraction patterns all have a fixed feature: the position of the beam-block. Therefore, some pixels in each diffraction pattern must be ignored in the computation of the cross-correlation.

Setting the ‘invalid pixels’ to 0 will not work, at those will correlate with the invalid pixels from the reference. One must use the masked normalized cross-correlation.

All of this is taken care of with the align() function. Let’s look at some polycrystalline Chromium:

(Source code, png, hires.png, pdf)

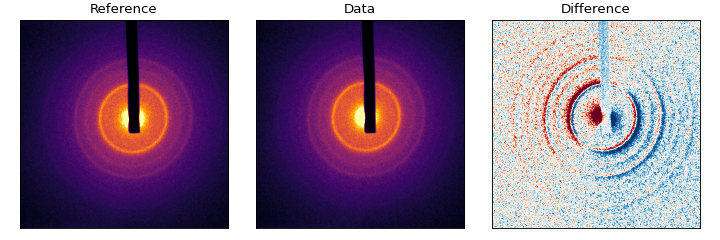
../_images/image-4.png

From the difference pattern, we can see that the ‘Data’ pattern is shifted from ‘Reference’ quite a bit, but the beamblock has not moved. To determine the exact shift, we need to use a mask that obscures the beam-block and main beam:

>>> from skued import diffread, align
>>> import numpy as np
>>>
>>> ref = diffread('docs/tutorials/data/Cr_1.tif')
>>> im = diffread('docs/tutorials/data/Cr_2.tif')
>>>
>>> # Invalid pixels are masked with a False
>>> mask = np.ones_like(ref, dtype = bool)
>>> mask[0:1250, 975:1225] = False
>>>
>>> aligned = align(image=im, reference=ref, mask=mask)

Let’s look at the difference:

(Source code, png, hires.png, pdf)

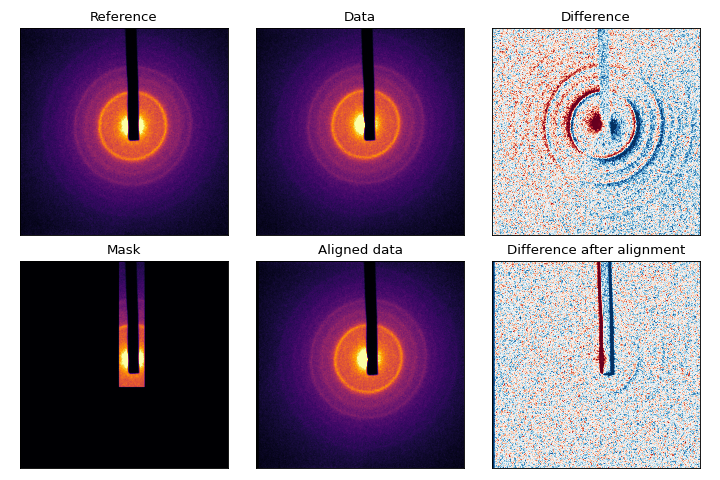
../_images/image-5.png

Image processing involving symmetry

Rotational symmetry

Diffraction patterns exhibit rotational symmetry based on the crystal structure. We can take advantage of such symmetry to correct images in case of artifacts or defects. A useful routine is nfold(), which averages portions of a diffraction pattern with itself based on rotational symmetry.

(Source code, png, hires.png, pdf)

../_images/image-6.png

To use nfold(), all you need to know is the center of the diffraction pattern:

>>> from skued import nfold, diffread
    >>>
>>> im = diffread('docs/tutorials/data/graphite.tif')
>>> av = nfold(im, mod = 6, center = (1024, 1024))    # mask is optional

Pixel Masks

Image data can be rejected on a per-pixel basis by using pixel masks. These masks are represented by boolean arrays that evaluate to Falose on invalid pixels, and True otherwise

scikit-ued offers some functions related to creation and manipulation of pixel masks.

Creation of a pixel mask

A pixel mask can be created from a set of images sharing the same properties. For example, diffraction patterns before photoexcitation (i.e. dark runs) form a set of images that should be identical.

Let’s imaging a set of such images with filenames dark_run_*.tif. We can create a pixel mask with the mask_from_collection():

>>> from glob import iglob
>>> from skued import mask_from_collection, diffread
    >>>
>>> dark_runs = map(diffread, iglob('dark_run_*.tif')) 
>>> mask = mask_from_collection(dark_runs)

In the above example, pixel values outside opf the [0, 30000] range will be marked as invalid (default behaviour). Moreover, the per-pixel standard deviation over the image set is computed; pixels that fluctuate too much are also rejected.

Note that since mask_from_collection() uses npstreams under the hood, the collection of files used to compute the mask can be huge, much larger than available memory.

Finding Bragg peaks

The first step in any single-crystal indexing routine is to find Bragg peaks. To this end, the bragg_peaks() function can be used as follows:

>>> from skued import diffread, bragg_peaks
>>>
>>> im = diffread('docs/tutorials/data/graphite.tif')
>>> mask = diffread('docs/tutorials/data/graphite_mask.tif').astype(bool)
>>>
>>> peaks = bragg_peaks(im, mask=mask)

We can plot the result:

(Source code, png, hires.png, pdf)

../_images/image-7.png

How cool is that!

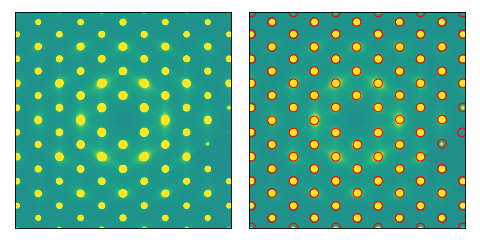
We can also use the method of 2D peak topological persistence to find Bragg peaks. Using the bragg_peaks_persistence() function, we determine the peaks via:

>>> from skued import diffread, bragg_peaks_persistence
>>>
>>> im = diffread('docs/tutorials/data/ab_initio_monolayer_mos2.tif')
>>>
>>> peaks, bd, bd_indices, persistence = bragg_peaks_persistence(im, prominence=0.1)

We plot the results. The left plot shows that the standard bragg_peaks() finds no peaks, while bragg_peaks_persistence() finds all of them, given on the right :

(Source code, png, hires.png, pdf)

../_images/image-8.png

Finding Brillouin zones

We can also determine Brillouin zones based on the location of Bragg peaks. For normal incidence diffraction, such patterns are regular polygons for simple crystal structures, but for tilted-incidence diffraction or macromolecules, the geometry becomes unclear, necessitating a different approach. The Brillouin zone, the Wigner-Seitz unit cell in reciprocal space, is also the Voronoi regions determined by the Bragg peak locations. This functionality is implemented in this package by the class brillouin_zones.

>>> from skued import diffread, autocenter, bragg_peaks_persistence, brillouin_zones
>>>
>>> im = diffread('docs/tutorials/data/ab_initio_monolayer_mos2.tif')
>>>
>>> peaks, bd, bd_indices, persistence = bragg_peaks_persistence(im, prominence=0.1)
>>> center = np.array([im.shape[0]//2, im.shape[1]//2])
>>> BZ = brillouin_zones(im, mask=np.ones(im.shape), peaks=peaks.astype(int), center=center.astype(int))

We can even determine equivalent scattering vectors at all visible Brillouin zones via the getEquivalentScatteringVectors() method, useful for averaging the signal at a given reduced wavevector for low SNR single-crystal datasets, visualized explicitly on the right.

(Source code, png, hires.png, pdf)

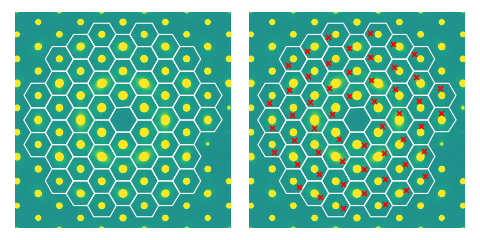
../_images/image-9.png

Image analysis on polycrystalline diffraction patterns

Angular average

First, let’s load an image:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from skued import diffread, autocenter
>>>
>>> image = diffread("docs/tutorials/data/Cr_1.tif")
>>>
>>> mask = np.ones_like(image, dtype = bool)
>>> mask[0:1250, 975:1225] = False
>>>
>>> plt.imshow(image)   
>>> plt.show()

(Source code, png, hires.png, pdf)

../_images/image-10.png

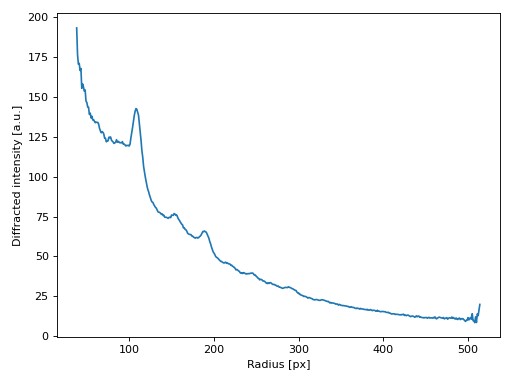
… and we can easily compute an angular average:

>>> from skued import azimuthal_average, autocenter
>>>
>>> yc, xc = autocenter(image, mask=mask) 
>>> radius, intensity = azimuthal_average(image, (xc, yc), mask=mask) 
>>>
>>> plt.plot(radius, intensity)

(Source code, png, hires.png, pdf)

../_images/image-11.png

Bonus : Removing Hot Spots

An interesting use-case of baseline-removal (described in Baseline-determination) is the removal of hot spots from images.

Consider the following diffraction pattern:

(Source code, png, hires.png, pdf)

../_images/image-12.png

We can consider the image without hotspots as the baseline of the image with hotspots :

>>> from skued import diffread, baseline_dwt
>>>
>>> im = diffread('docs/tutorials/data/hotspots.tif')
>>> denoised = baseline_dwt(im, max_iter = 250, level = 1, wavelet = 'sym2', axis = (0, 1))

The result is plotted below:

(Source code, png, hires.png, pdf)

../_images/image-13.png

Try different combinations of wavelets, levels, and number of iterations (max_iter).

Notice that the baseline-removal function used in the case of an image is baseline_dwt(), which works on 2D arrays. The same is not possible with baseline_dt(), which only works on 1D arrays at this time.

Return to Top